Molecular Weight Control in Step-Growth Polymerization

The molecular weight of a polymer is one of the most important parameters because it controls, to a large extent, the final mechanical and thermophysical properties such as glass transition temperature, melt and solution viscosity and mechanical strength, to name only a few properties. For many applications, a high molecular weight is desired. However, polymers with high molecular weight can only be obtained by step-growth when three critical requirements are met: First, the two difunctional monomers (A-A & B-B) have to blended at perfect stoichiometric balance. In other words, the ratio of the concentrations of the reactive groups, r = [A] / [B], has to be equal or very close to 1.0. In the case of a single A-B type bifunctional monomer such as an amino acid or hydroxy acid, this balance is automatically provided. Second, monomer impurities that can react and terminate step-growth have to be kept at an absolute minimum because any trace amount of a monofunctional reactive compound will cap the growing polymer chains and thus reduce the molecular weight. However, stringent purification of the reactants is often difficult and adds cost to the final product. Third, the step-growth polymerization has to be driven close to completion, i.e. to a very high yield without any side reactions.

The molecular weight of a step-growth polymerization can be easily calculated if we assume that each functional group has the same probability of reacting with other groups regardless of the size of the oligomer and type of functionality. This assumption is called Flory's equal reactivity principle. According to this principle, the probability that a given reactive group has reacted at time t is equal to the fraction of monomers p that have undergone condensation which is called the extend of the reaction.1 Then the average degree of polymerization (DP) is equal to the total number of bifunctional units initially added N0 divided by the remaining number of molecules N:2-5

DP = N0 / N = N0 / N0(1- p) =  1 / (1- p)

Consider a reaction that can be driven to 90% completion which is a relative high yield and not easy to achieve in a bulk polymerization. Then the average degree of polymerization DP is 1 / (1-0.9) = 10. However, a decamer is to short to have useful mechanical properties. In general, the molecular weight has to be about two times the entanglement weight which equals about 15 to 100 repeat units, depending of the structure of the molecules.9 For example, to obtain a DP = 50, polymerization has to be carried out to 98% completion, DP = 1 / (1-0.98) = 50. Therefore, a relative high conversion is required to attain a high degree of polymerization.

As has been pointed out by Flory5 and many other scientists, the true average degree of polymerization is often lower than the theoretical value. The main reasons for this discrepancy are threefold: a) some monomer may evaporate during polymerization, b) some monomer may undergo side reactions, and c) (trace amounts) of monofunctional reactive compounds could be present. This will lead to a stoichiometric imbalance of the number of reactive groups A and B and a depression of the average molecular weight.4,5

Stoichiometric Imbalance of Bifunctional Monomers A-A and B-B

The stoichiometric imbalance is defined by the ratio r = NA,0 / NB,0, which cannot exceed unity by definition. Then the total number of reactive units is

(NA,0 + NB,0) / 2 = NA,0 (1 + 1/r) / 2

where NA,0 and NB,0 are the total number of A and B groups initially present. The number of unreacted A and B groups after the reaction has reached extent p is

NA,0 = (1 - p) NA,0
NB,0 = (1 - p r) NB,0 = (1 - p r) NA,0 /r

and the total number of chain ends

(1 - p) NA,0 + (1 - pr) NA,0 /r = (1 - 2p + 1/r) NA,0

which must equal twice the total number of molecules since each molecule has two terminal functional groups. The number average degree of polymerization DP equals the number of repeat units divided by the number of chains:4,5

DP = (1 + r) / (1 + r - 2pr)

At 100 % conversion (p = 1), this expression reduces to

DP = (1 + r) / (1 - r)

 

Number-Average Degree of Polymerization as a Function of the Stoichiometric Ratio

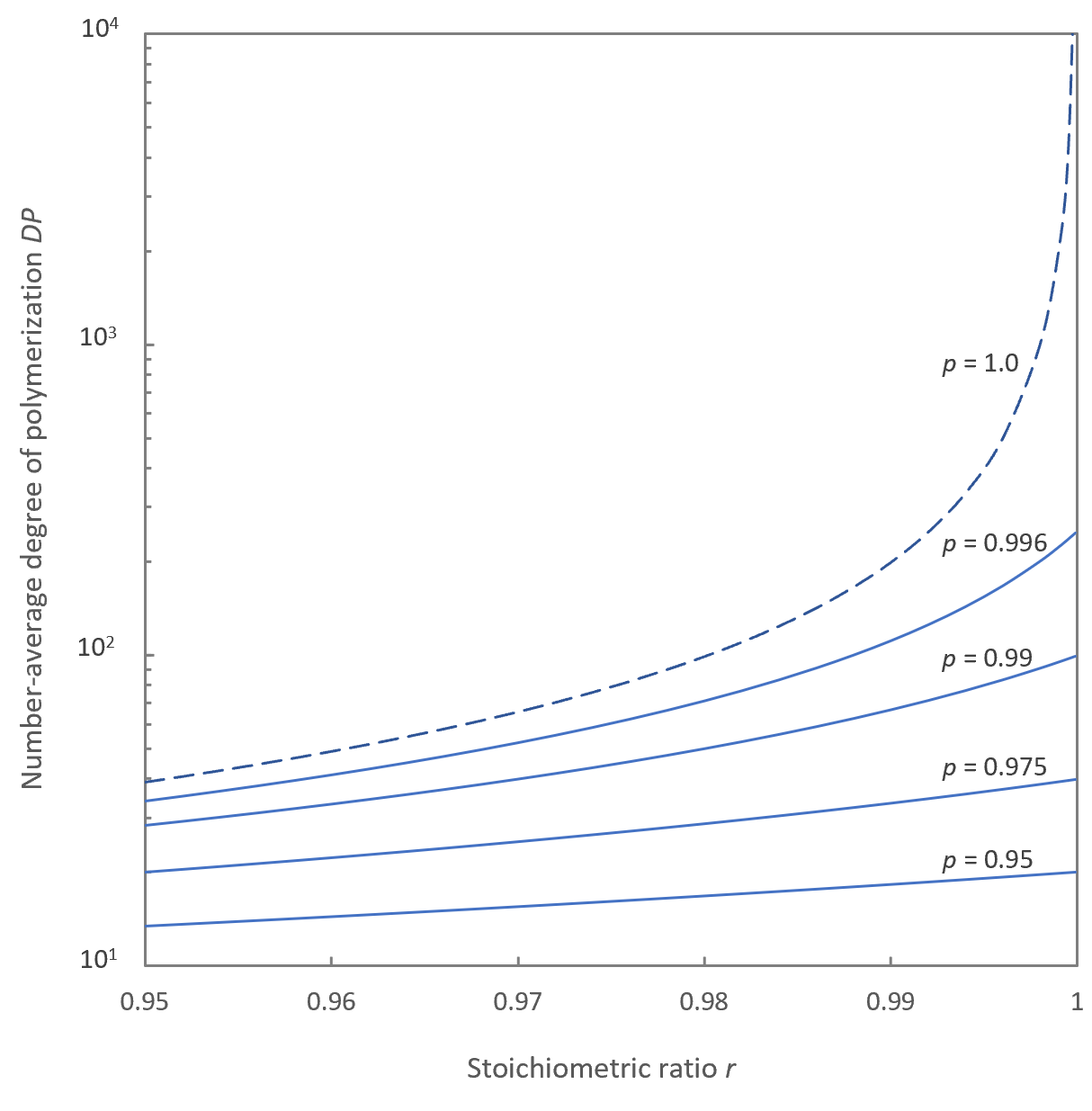
The Figure above shows the effect of stoichiometric imbalance and conversion on the average degree of polymerization. The DP drops with increasing stoichiometric imbalance and decreasing conversion. For example, an excess of 1% of B-B monomers reduces the degree to polymerization to about 100 units. Thus, a small loss of reactant through evaporation of A-A or B-B monomers or through side reactions can substantially limit the molecular weight of the final product. If, in addition, the polymerization is carried out to 99% completion instead of 100%, the degree of polymerization will reduce to 50 units. Thus, to achieve a high DP, the reaction has to be driven close to completion.

Depression of Molecular Weight by Monofunctional Reactants

The addition of a monofunctional reactant or impurity to an equimolar mixture of A-A and B-B monomers will depress the molecular weight through end-capping. As Flory has shown, the same equations can be applied to this situation if r is redefined as follows:5

r = NA,0 / (NB,0 + 2NB,1) = NA,0 / (NA,0 + 2NB,1)

where NB,1 is the initial number of monofunctional B monomers. The factor 2 arises here because a B molecule has the same quantitative effect in limiting the molecular weight as one excess B-B monomer. With this definition, the plots above describe the depression of the molecular weight by  monofunctional monomers as well.

Change of Molecular Weight by Trifunctional Reactants

Branched polymers can be formed when some of the monomers have three or more functional groups per molecule. However, the addition of trifunctional monomers can also generate cross-linked polymers (polymer gel). In other words, a step polymerization involving trifunctional units can lead to the formation of insoluble cross-linked structures (gel fraction) embedded in linear and branched polymers (sol fraction) or to an infinite insoluble polymer network that is, to one gigantic molecule. The point in the polymerization at which the polymer starts forming crosslinked structures (insoluble gel) is called the gel point. According to Flory, an infinite network becomes possible when at least one of the functional groups of the f - 1 branches has reacted with a functional group of another branch. The probability αc of this occurring is 1 in f - 1 or,5-7

αc = 1 / (f - 1)

Therefore, when trifunctional branch units are involved, infinite networks are possible only when α ≥ 1/2.8 The point in the polymerization at which the polymer starts to form a crosslinked structure will depend on the degree of polymerization, the fraction of trifunctional monomers, and the stoichiometric ratio of A to B groups. According to Flory (1941) the number average degree of polymerization and the fraction of monomers in branched units can be calculated from7

DP = [f(1 - ρ + 1/r) + 2ρ] / [f(1 - ρ + 1/r - 2pA) + 2ρ]

α = (rpA2ρ) / [1 - rpA2(1-ρ)] = (pB2ρ) / [1 - pBA2(1-ρ)]

where ρ is the ratio of A groups belonging to branched molecules to the total number of A groups, r is the stoichiometric ratio of A to B groups, and pA equals the fraction of A's which have reacted. Combining the last expression with αc = 1 / (1 - f), gives following equation for the extent of reaction of A groups at the gel point:

pc = 1 / {r [1 + (f - 2)]1/2}

For a difunctional resin reacted with a trifunctional resin, the critical branching coefficient is αc = 0.5 and the critical extend pc = (0.5)0.5 = 0.707 (r = 1, p = 1). Thus, gelation occurs at a conversion of 70.7 %. In practice, gelation often occurs at higher values. This deviation has been ascribed to the fact that the functional groups on multifunctional monomers can have different reactivities.6

References  and Notes

  1. In the case of functional end groups, like amine or acid groups, the probability p can be directly calculated from the end group titer, i.e. in the case of a polyester from the carboxyl group titer. For example, assuming a third-order reaction, the reation can be written in the form 2kt = 1/c2 - 1/c02 (see Step-growth polymerization), where c is the carboxyl group concentration and c0 its initial value. If the extend of reation is equal to the probability p that a carboxyl group is esterified then (1- p) = c / c0  or  2c02kt = 1 / (1- p)2 - const. This means, a graph of (c0 / c)2 versus time, t, should yield straight lines from which p can be calculated.

  2. This equation was originally suggested by Carothers in 1936 and is often referred to as the Carothers equation.5

  3. Wallace H. Carothers, Trans. Faraday Soc., Vol. 32, pp 39-49 (1936)

  4. P. J. Flory, Journal of the American Chemical Society, 58, 1877-1885 (1936)

  5. Paul L. Flory, Principles of Polymer Chemistry, Ithaca, New york (1953)

  6. J. K. Stille, J. Chem. Educ.,58 (11), pp. 862-866 (1981)

  7. P. J. Flory, J. Am. Chem. Soc., 63, 3083 - 3090 (1941)

  8. If p and r approach unity, i.e., if all groups belong to branch units, then α = p

  • Summary

    Step-Growth Polymerization

    is a stepwise reaction between polyfunctional monomers by various condensation and addition reactions in which high-molecular-weight polymers are formed after a large number of steps.

  • Oligomers and polymers of any length exist throughout the reaction, with the length distribution broadening and shifting to higher molecular weight with increasing extend of reaction.

  • Low molecular weight oligomers and polymers are most abundant throughout the polymerization unless the reaction has been driven close to completion at (nearly) stoichiometric amounts of reactants.

  • The observed average degree of polymerization is often lower than the theoretical value. The main reasons for this discrepancy are threefold:

    a) some monomer may evaporate during polymerization,
    b) some monomer may undergo side reactions, and
    c) monofunctional reactants could be present, often referred to as chain stoppers.

  • The number average degree of polymerization decreases monotonically wih increasing stoichiometric imbalance.

  • The addition of a monofunctional reactant (A or B) to an equimolar mixture of A-A and B-B monomers has the same quantitative effect in limiting the molecular weight as the addition of the same amount of a bifunctional monomer (A-A or B-B).

  • A step polymerization involving trifunctional units can lead to the formation of insoluble cross-linked structures (gel fraction) embedded in linear and branched polymers (sol fraction) or to an infinite insoluble polymer network

  • Gelation occurs in network polymerization long before all of the polymers have reacted to one large molecule (gel).

  • Network polymerization is characterized by a sharply defined gel point at a certain critical extent of reaction which is not affected by temperature, amount of catalyst etc.